
HOME >> 鉄道模型工学 > 鉄道模型工学概論 > 動力特性の基本式 車両特性
鉄道模型工学概論 動力特性の基本式 車両特性
§1.5 車両特性
つぎに車両として全体を見た時の特性を考えてみる。
ここで、今までの関係式を整理することになるが、その関係は複雑となり、全体像が把握し難くい事となる恐れがある。そこで、その関連を容易に理解するために、関係式をブロック図として表示してみる。 ブロック図は自己流であるが、エネルギーフローの概念を取りいれ、要素ブロックを4端子ブロックで表示し、 要素としては、モータ部、減速機部、車両部の三っつの部分に分けてブロック化している。
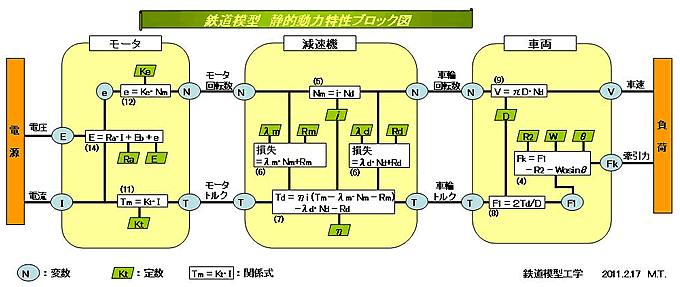
⇒ 拡大図
電源から電圧×電流として供給されたエネルギーは、モータによって回転数×トルクと変換され、減速機と車両によって、車速×牽引力となり、負荷に伝達される。 そして、途中で色々な損失によって失われるが、最終的には負荷でそのエネルギーは消費されることになる。
そして、供給側の電圧と電流、および消費側の車速と牽引力の関係は、そのブロック図の線図をたどっり、関係する10個の関係式を結んでいけば良い事になる。 特性を決めるそれぞれの定数が、どの変数に影響するかもビジュアル的に追っていくことも出来る。
それでは、最初に牽引力と車速の関係を、電圧をパラメータとして表現してみよう。
まず、式(8)に式(7)を代入して、駆動力 F1 とモータトルク Tm の関係を求める。
![]()
この式(18)に、式(11)、式(14)、式(12)、式(5)、式(9)を代入し、駆動力 F1 と車速 V との関係を求める。
![]()
さらに式(4)に代入し、牽引力 Fk の基本式を求める。
<< 牽引力の基本式 >>

動力車の牽引力は、速度によって減少する垂下特性を示すと共に、電圧によっては比例的に増加する。 また、各種の摩擦損失などによってモータで発生したトルクが失われると共に、坂道においては自分の重量による勾配抵抗も大きく作用する。
また、牽引力と電流の関係を、電圧をパラメータとして表現してみよう。
まず、式(18)に、式(11)を代入するとともに、NdとNmを、式(5)、式(12)、式(14)を使用して電圧Eをパラメータに表現し、牽引力 Fk と電流 I の関係を求める。
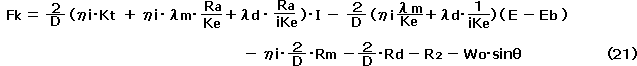
なお、この他に、曲線路走行時の抵抗など配慮すべき項目はいろいろあるが、それらは無視している。
**************************
この牽引力の様子を知るためには、この特性をグラフ化してみると理解しやすい。 そして、測定されたデータをグラフ化する場合にも、このグラフと同じ座標で表示出来れば、対象とする模型車両の特徴を視覚的に捕えることが出来る。また、測定する条件に合わせて検討しておけば、測定データのグラフが示す意味合いも理解出来る。 そして何よりもそのデータから読み取る事の出来る色々な係数を理解する手助けともなる。
そこで、次の状態で検討を行うことにする。
1) 平坦路走行状態とする。
レイアウトでは登坂や下り坂を設ける事が多いが、ここでは、その勾配抵抗については、考慮しないことにする。 その理由は、勾配抵抗の影響の仕方がシンプルなので、複雑化を避けるためである。 車両重量と勾配角度が分かれば単純に計算することができるからである。 平坦路走行状態、即ち θ=0 の状態で検討することにする。
2) 進行方向は前進のみを考える。
また、進行方向についても、基本的には対称と考えられるので、正行(前進)状態のみを考える。
3) カプラーを介して車両に掛る力は正負を考える。
牽引力 Fk については、正負を含めて考え、正の場合は駆動状態、負の場合は制動状態を示す。
4) 単機走行状態も検討する。
平坦路を動力車のみで走行している場合を考えて見よう。 でも、これは “ 特殊 ” な場合とは言えないだろう。 SLやELなどの機関車類を購入した場合、まず、単機で走らせ、その走り具合いを胸躍らせ、目を凝らして観察するはずである。 このような状態は、平坦路でかつ単機での走行状態となる。
5) モータ単品状態も検討する。
本来なら、モータ単品状態での性能測定は、基本中の基本であろう。 しかし、その測定はトルク計や回転計など、特殊で専用的となる装置を使用しなければならない。 ここでは、単に電流と電圧だけを測定した場合に、何が分かるか検討してみる。
6) 測定する要素

今回、簡易な装置で測定可能な要素として、牽引力 Fk 、車速 V 、電圧 E 、電流 I を取り上げ、さらにギヤ比、重量、寸法なども計測可能な諸元である事を前提にして、解析する。
なお、新しく使用する変数を右に示す。
この牽引力の様子を理解するため、グラフ化してみる。 ここで、勾配抵抗は、影響の仕方がシンプルなので、複雑化を避けるために平坦路走行状態、即ち θ=0 の状態で検討する。 また、進行方向についても、基本的には対称と考えられるので、正行(前進)状態のみを考える。
ただし、牽引力 Fk については、正負を含めて考え、正の場合は駆動状態、負の場合は制動状態を示す。
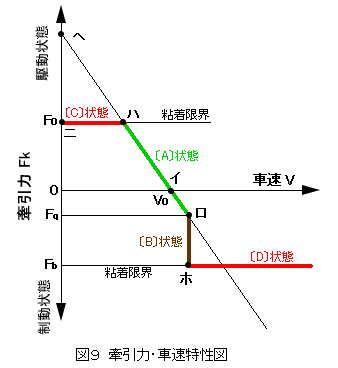
まずはじめに、 図9のように横軸に車速 V 、縦軸に牽引力 Fk とし、 ある一定電圧 E と仮定して式(20)をグラフ化する。
即ち、式(20)の特性は、へ点を Y切片とする右下がりの直線となる。 この直線の勾配は、速度項の係数で決まるので、式(20)に示すごとく一定の値である。 即ち、勾配は変化しない。 電圧 E は、この直線を平行に移動させるパラメータとして示すことが出来る。
そして、牽引力がゼロの状態、即ち、単機での走行時にはイ点の状態となる。 その時の車速を無負荷走行車速 Vo とする。
この通常走行状態では式(20)が成立しており、ウオームギヤの状態は(A)の状態である。
他の動力車から押されたり、下り坂などで自重を含めて後ろから押される場合には、この動力車には負の牽引力(制動力)が作用する。 この場合はイ点から下にさがるが、ロ点までは、動輪や従輪の摩擦抵抗で対応するため、依然として式(20)が成立している。 従って、直線上を変化していく。 しかし、それ以上の力が要求される場合には、§1.3 で述べたごとく、力を保持しながら回転する(B)の状態に突入し、そして、式(20)はもはや成立しないと考えるべきである。 どのような特性になるかは未検討であり、多くの観測と実験データが必要と思われるが、ギクシャク運転の不安定状態とも推察される。 ここでは、垂直な直線で表現しておく。
また、ロ点をしめす時の力は、ウオームホィールを含めた動輪や従輪の摩擦抵抗で対応しているため、制動力 Fq は、
![]()
となるであろうと想定するが、 いろいろな要素が関係するとおもわれるので、実際のところよくわからない・・・・・・・。
次に、より高い牽引力を必要とする場合には、イ点より上方に移行し、モータのストール状態であるヘ点に向けて車速を減少しながら移動していく。 しかし、車輪とレールとの間の粘着力には限界があり、ハ点以上は車輪が滑って力を発揮することが出来なくなる。 そして車輪のスリップ状態であるハ点とニ点間に突入し、場合によっては車速ゼロの状態まで落ち込んでしまう。 そしてモータはハ点だが、車体はニ点にあるという車輪の空回り状態が(C)の状態と言える。
この粘着限界での不安定な状態の牽引力が、一般に言われている“牽引力”であり、もはや式(20)は成立しない。また、その時の車速を規制する要素は、不確実であるため、ハ点とニ点の間はバタバタした状態となろう。
一方、制動側には粘着限界が存在し、ロ点から制動力を大きくするとその限界点ホに達する。そして車体は、車輪の回転数以上にレールの上を滑って行くことになる。
自動車に詳しい方は、ブレーキを掛け過ぎると車輪がロックしてしまい、車体のコントロールを失ってしまう危険な状態に陥ることはご存じと思われる。 このためにわざわざ車輪がロックしないように制御しているABSなる装置があるのであるが、鉄道模型の世界ではABS装置が無くても、どっこい車輪は回転しているのである。 ブレーキ構造の違いかな。 ちなみに実際の機関車や電車の場合は、原理的には自動車と同じブレーキ構造であるため、 車輪の摩擦限界(鉄道系では粘着限界と言っている)を超えると車輪はロックするものと思います。
さて、駆動側の粘着限界と制動側の粘着限界は、同じ値になると思われるが、車輪の回転状態が異なるので実験してみないと分からない。
ここで、粘着限界Foは、粘着係数をμとすると、
![]()
で表わされる。 従って、車両重量 Wo を重くすると W1 も増加し、駆動力 Fo を大ききすることが出来る。 これはモータ特性とは無関係なので、車体に重りを付け足すなどの加重を実施して、(C)状態の線を上方に引き上げることによって駆動力 Fo を大ききすることと共に、通常状態の(A)の範囲を広くする効果も生まれる。 ただし、車両重量を重くすることは、自分自身の勾配抵抗を増やすことであり、坂路の多いレイアウトでは考慮が必要である。
車両重量ではなく、粘着係数μをアップさせることによっても駆動力を向上させることが出来る。 鉄道模型に於いては、動輪にゴム環を履かせてμをアップさせたり、動輪の数を増やしたりして車両重量を有効に使用する方法など、駆動力を大きくする工夫がされている。
■ 粘着限界は安全弁
この粘着限界は、鉄道模型の安全弁と考える事が出来る。 モータの設計で注意することはその焼損対策が重要であると聞いたことがある。 巻線が“電熱器”となって発熱・発火して、やけどや火災になる恐れがある。 鉄道模型と言えどもモータが熱くなる事はご存じの通りであり、焼損してしまったと言う話も聞く。 もし火災となれば製造者責任を問われかねない。
一般に、小型モータでは制約されたスペースの中で、最大限の力が発揮できるようにぎりぎり設計が求められる。 このため、1分定格とか、3分定格など、短時間での使用を想定した設計方針が取られる事が多い。 この場合には、タイマーとか、熱センサーでモータを監視しつつ、モータを駆動する制御が施されている。 また、ヒューズブルリンクなどの安全機構が取り入れられている。
では、我々の鉄道模型では、どうだろうか? モータは何分定格なんて明記されていなし、使用状態を考えると “連続定格” が求めれれている。 ヒューズは? パワーユニットにはあるようだが車両にはその配慮は見当たらない。 では、不安全か? いや、この粘着限界が安全弁となって作用してくれるのである。 モータの異常な発熱の恐れがあるヘ点のストール状態を回避してくれているのが、(C)状態の存在である。
また、駆動ギヤについても、駆動力を(C)状態に抑えてくれるので、ギヤに掛る力を制限してくれることににもなっている。 このため、やたらに重りで車両重量を増やしたり、ゴム動輪を増やしてして粘着力を大きくすることは、この安全弁を緩めていることになる事を認識しておこう。 でも、ぎりぎり設計をしている様には見えないので、そう心配することも無いと気楽に考えている。
次に、牽引力と電流との関係を見てみよう。 走行条件は上記の牽引力・速度特性と同じである。
式(21)において、θ=0 の状態とすれば、牽引力 Fk と電流 I の関係が求められる。

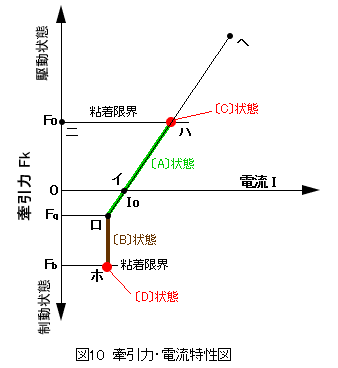
特性式(21-1)を縦軸を牽引力、横軸を電流として、図9と対応を取って図10に示す。
牽引力が無負荷状態の単機走行状態はイ点で示される。このイ点より下方は制動状態に入るが、車輪系の摩擦抵抗で対応するため、モータの負荷が減少し、その結果として電流も減少していく。
さらに制動力が要求されるとウオームギヤ部の状態が変化し、(A)状態から(B)状態へと変化する。 その後のモータの負荷状態はよくわからない。 ここでは、一定負荷の状態で回っていると仮定している。
イ点より負荷が大きくなった場合、牽引力の増加に合わせて電流も増加していく。 そしてモータのストール状態のヘ点へ達する前に粘着限界ハ点に達し、この(C)の状態を保持するものと思われる。
式(20)の特殊な場合として、平坦路を動力車のみで走行している場合を考えて見よう。 でも、これは “ 特殊 ” な場合とは言えないだろう。 SLやELなどの機関車類を購入した場合、まず、単機で走らせ、その走り具合いを胸躍らせ、目を凝らして観察するはずである。 このような状態は、平坦路でかつ単機での走行状態となる。 さてその走り具合を特性面から見てみよ。
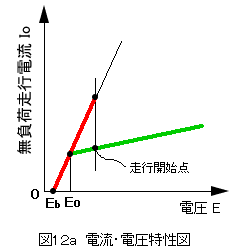
平坦路・単機走行状態であるので、Fk = 0 、θ = 0 の状態である。 変数は、電圧 E と、それによって影響される車速 V および電流 I の3変数となる。 式(20)より、Fk = 0 、θ = 0 の場合の車速 V を、無負荷走行車速 Vo とすると、
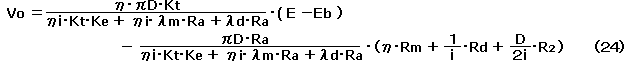
で示される。 ここでさらに、Vo = 0 となる電圧 E を Eo とすると、
![]()
となる。
式(24)をグラフに示すと図11の様になる。 車速 Vo は、Eo 点から右上がりに、一直線で示され、その勾配は上記の様に多くの要素が関係してくる。
そして、電圧 E がEo よりもある程度上昇した時点で初めてモータは回り始め、車両は動き始める。 これを走行開始点としてグラフに示す。 これは、DCマグネットモータでは、一般的に生じる現象であり、強力磁石を用いた高性能モータでは、特に顕著に見られる。 磁石が回転子の鉄片を拘束しているためと自分は解釈している。 これは、鉄道模型でのラビット・スタートの原因ともなっている。 なお、一度回りだせばこの開始点より低い電圧でもスムーズに回っている。
なお、この無負荷走行車速 Vo は、図9の牽引力・車速特性図に示すイ点の車速を表わしている。
さらに、電流と電圧の関係を見て見る。Fk = 0 、θ = 0 の状態のモータのトルクを式(4)、式(7)、式(8)より求める。
![]()
1) モータが回っていない ( ロックしている ) 場合:
モータが停止あるいはロックしている場合は、Nm = 0 であるため、式(12)より e = 0 、即ち逆起電力がゼロとなる。 すると式(14)より、無負荷時の走行電流 Io は、
![]()
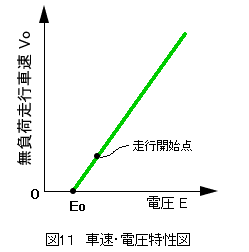
となる。 これは、モータが電気的には単なる抵抗体となっていることを示している。 いや、電熱器といっても過言ではない。 発熱に要注意である。 この状態を線図に示すと、図12aに示す電流・電圧特性図の赤線の様になる。Eb点を起点に、勾配 1/Ra で立ち上がっている。 オームの法則そのものである。
2) モータが回転している場合:
モータの負荷は式(26)の状態であるため、式(11)と式(16)より、無負荷時の走行電流 Io を求める事が出来る。 式が複雑となるため、
![]()
と新たな係数を設定して式を整理する。
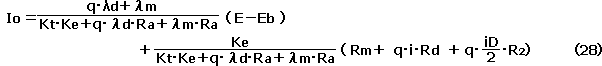
となる。 この式は、走行電流 Io が電流 E と比例関係にあることを示している。 特性線図に示すと、図12aの緑色の線で示される。 赤線との交点は、モータ回転数がゼロ以上になる点で、その時の電圧は Eo となる。 また、図11で示した走行開始点は、この Eo 点よりも高い電圧となり、この間は回転数がゼロであるため、赤線沿いに電流は増加することとなる。
つぎに、モータ単品状態での電流と電圧の関係を見てみよう。 モータ単品状態では、モータ軸回りの損失のみを考えれば良いので、
![]()
とすると、式(11)、式(14)、式(12)より、 I = Io とすると、
![]()
の関係を得る。
ここで、式(28)と式(30)を比べてみよう。 式(28)に於いて、q=0 と考えれば式(30)になることが分かる。 q=0 とは、ギヤ比 i が無限大になり、駆動輪側の負荷抵抗の影響が無限に小さくなること、 即ち、無きに等しいことを意味する。 従って、その状態はモータ単品状態の式(30)と同じと言う事である。
そして、特性図は図12aと同じであることが言えよう。
*******************************