HOME >> 鉄道模型工学　>　μカーブから発進特性を考える　その１

鉄道模型工学　μカーブから発進特性を考える　その１

　 いつも愛読しているさるブログの「物理実験」という記事に注目しているが、いろいろな点で懸念を持ってしまった。そこで、関連する項目について振り返って考察することにした。今回は粘着特性であるμカーブと、それと関連する項目について、復習と考察をまとめてみた。

 

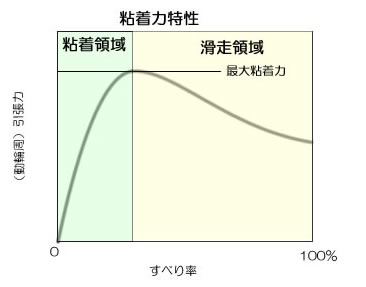
■ μカーブについて

　自動車屋の自分は、現役時代にこの用語をよく見聞きしていた。この「μカーブ」とは、タイヤと路面の関係を示す基本特性であり、スキッドコントロール（ABSなど）やトラクションコントロールの制御理論の基本となっている特性カーブのことである。

　一方、鉄道関係ではタイヤが車輪に、路面がレールに変更したと考えれば、特性の基本的考えは同じと言えよう。鉄道の場合、ウィキペディアによると車輪とレールの接触現象を「粘着現象」と言っている。

　　　　　******** 　「粘着式鉄道」　*******

　そしてこのμカーブ特性を右のような特性として紹介されている。具体的な数値としてはかなり異なるものの、自動車の場合と鉄道の場合の特性の傾向と特徴は同じと言えよう。

 

●すべり率について

　今回、改めて確認した項目として、横軸となる「すべり率（スリップ率）」の定義の内容である。上記の説明では、”すべり率は、円周速度と車両速度の差を車両速度で割った値として定義される。” と記述されているが、ここで注意すべき点は、発進時の車速はゼロなので、割算の分母として使えないのである。この内容では定義出来なのである。

　　　*****************************************************

　　.

　では、自動車の場合はどうだったのだろうかと、昔勉強した教科書を持ち出してきた。 近藤政市工学博士著「基礎自動車工学 −前期編-」 昭和42年第３版、養賢堂出版である。その 111ページの一部のコピーを右に示す。

　さすがに大先生であり、ブレーキ状態とトラクション状態を明確に区別して定義されていました。

　今回は発進時の挙動を考察するので、ブレーキング時の状態を検討する被制動車輪の場合でなく、動輪による駆動状態を検討するので、トラクション状態、即ち、被駆動車輪の場合の式を使用し、

で定義したすべり率をλとすることにします。

　これによって、発進時の車速ゼロの場合もデータが整理出来るのである。

　ちなみに、小生が鉄道模型工学として今まで使用してきた内容は、スリップ率について考察する（2014/12/25）にて記述している。スリップ率をβ、車速をV 、動輪直径を D 、動輪の回転数 Nd、とすると、

　　　　　　　　

としている。すべり率の記号はあえて変更しているが、πD・Ndは円周速度なので、式を変形すると同じ式になることが分かる。　よかった-------！。従って今までの記述は間違っていなことが確認でき、安心して議論を進めることが出来ます。

 

●引張力について

　この（動輪周）引張力は、車輪とレールの間に働く摩擦力を示し、垂直抗力に擦係数を掛けた値として求めることができる。そして、垂直抗力は車輪に掛かっている車体の重量（輪重）なので、その値が決まればこの引張力は求められる。

　但し注意しなければならない事は、モータのような動力源ではないので自分で発生する力ではない事である。これはあくまで、動輪に伝えられた力を伝達する能力を示しているに過ぎない。モータなどの駆動力や動輪のブレーキ力が不足している場合には、その力しか伝達しないのである。地面に固定されたレールと空間を移動する車両の間を連結する一種のクラッチ機構なのである。そしてその伝達できる能力を示しているに過ぎないのだ。

 

■ 粘着領域での挙動

　まず、このμカーブの特性を理解するため、走行中の駆動状態で、かつ、状態が安定している粘着領域での挙動を見ていこう。

　さらに、下記に示す車両挙動を考える場合、動輪を回転させる駆動トルクは、充分に余裕のある能力を持っているとする。即ち、モータやエンジンのパワーは充分発揮できるパワーを有しているとする。しかし、その時に発揮しているパワーは、作用・反作用の原則により、負荷に応じたパワーしか出していないのである。

 

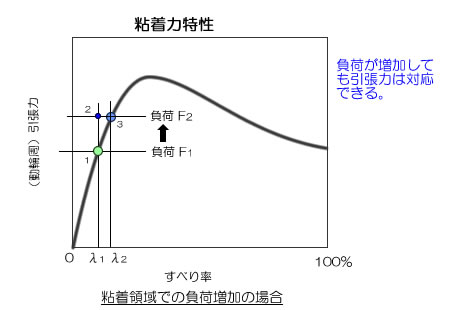
●負荷が増加した場合の挙動

　すなわち、負荷が増加しても引張力はそれに対応するので安定した状態を保って走行できることを示している。

 

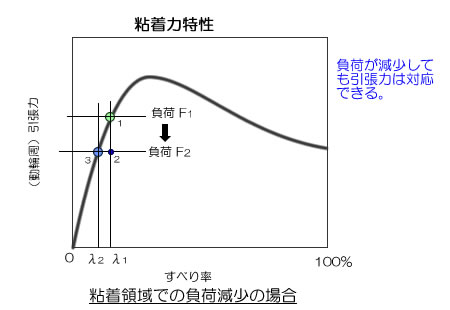
● 負荷が減少した場合の挙動

　すなわち、負荷が減少しても引張力はそれに対応するので安定した状態を保って走行できることを示している。

 

●ま とめ

　上記の負荷の増減に応じて引張力の伝達力は増減することになり、これによって安定した走行を維持できることを示している。

　もし、モータなどの動輪の駆動トルクが小さい場合、その時の駆動源の駆動力-速度特性に応じた車速となり、すべり率もそれに応じた状態になっているのだ。

 

■ 滑走領域での挙動

　次に、滑走領域での挙動を見ていこう。この領域では安定した状態を保持できないので、滑走領域と呼ばれる所以である。そこで、ある状態の時から変化具合に注目して考えてみよう。すると、何故安定しないのかが理解できるのだ。

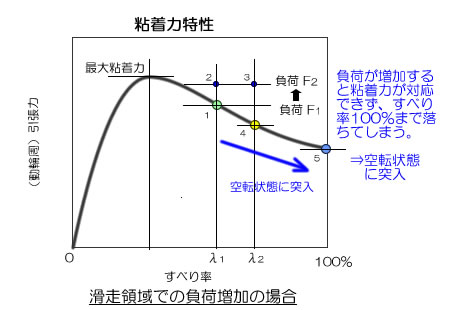
●負荷が増加した場合の挙動

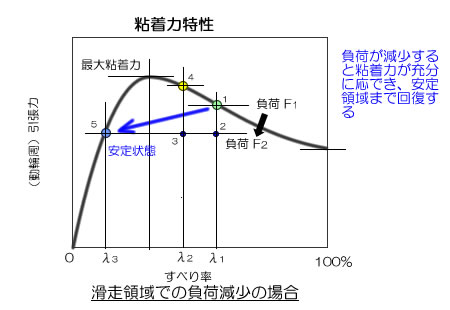
● 負荷が減少した場合

● まとめ

　この滑走領域での挙動は不安定な領域ですが、現実ではいろいろな場面で遭遇するのです。タイヤがスタックしてしまい動かなくなる、動輪が空転して発進できない、あるいは峠を越えることが出来ない、雪道でブレーキを掛けたらスリップして崖から落っこちた、などなど、多くの問題を抱えていた。そして、関係する技術者は、長年克服しべき技術課題として研究と改良を進めてきた分野なのです。

　その解決方法とは、ABSとか再粘着制御など、コンピュータを用いた制御システムにより、不安定領域をいかに克服するのか、いろいろな手法を使って安定状態になるように制御する高度な技術分野なのです。

　　*********************************************

　上記のような考察を検討している時、ブレーキング状態なのかトラクション状態なのか自分でも混乱してしまいました。

　この二つのケースではすべり率の式が異なっていますので、負荷の増減とすべり率の増減方向に注意する必要があります。でも、結果としてすべり率が100％の場合は問題状態なので、いろいろな弊害をひき起こしているのです。

 

　　*********************************************

　前置きが長くなってしまったが、次回はμカーブの挙動を理解したつもりで、発進時の挙動を考えてみよう。