
HOME >> 鉄道模型実験室 > DCモータのブレーキ特性 特性の解析 その2
鉄道模型実験室 No.265 DCモータのブレーキ特性 特性の解析 その2
DCモータのブレーキ制御方法について、実際の実験装置を使って確かめる事にしよう。先回の報告で指摘した「摩擦損失速度係数 λm は無視できない値である」ことを踏まえ、関係式の再整理を実施してDCマグネットモータのブレーキ特性の解析することにした。そして、実際のデータを解析してみた。
■ ブレーキ回路のデータ
測定は、「DCモータのブレーキ特性 RE-260RAのブレーキ特性」(2025/12/2)に従って実施した。そして、得られたExcelのシートの一部を下に示す。
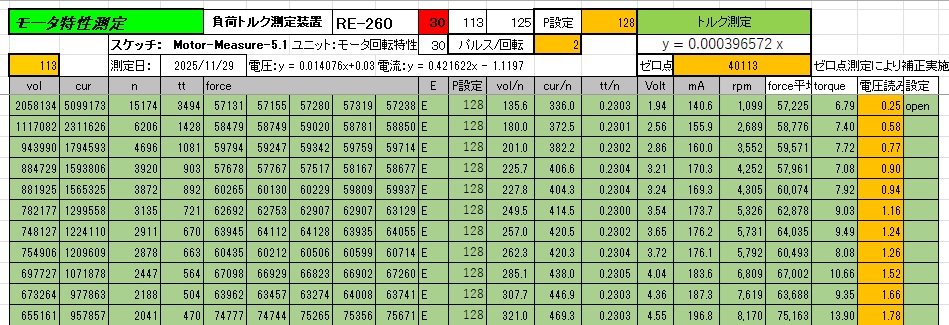
設定状態は右端の「設定」欄に内容を記入しておく。そして、その左の欄の「電圧読み」欄にテスターで読み取った値を測定のたびに手入力していく。ただし、ショート状態のときは回路の抵抗がほとんどゼロのために読み取れ無かったので記入していませんでした。
回路の抵抗をボリュームで調整して、8.0 Ω、.4.3 Ω、2.6 Ωに選択して測定を実施した。100 Ωの可変抵抗しか無かったので微少の値の設定が難しかった。予想はしていたが、今後は改善する必要がありますな。
● 測定データの概要
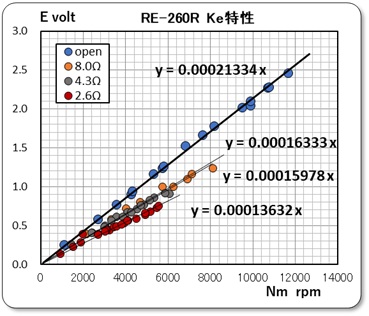
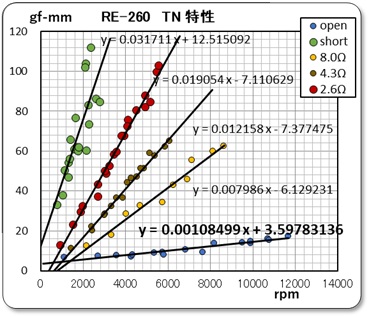
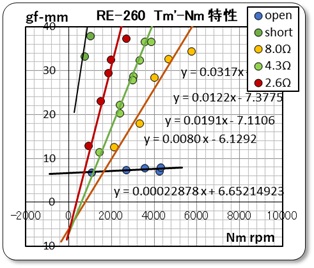
得られたデータをまずグラフに示しておこう。下左の写真は、先回に報告した逆起電力定数の測定時のデータに、他の状態のデータを追加した電圧-回転数特性のグラフである。また、右のグラフは、この時のトルク−回転数のグラフである。
グラフ 1 グラフ 2
■ 発電ブレーキとして制御できる範囲
次に、モータ特性の説明でよく使用されている 回転数−トルク と、電流−トルク のグラフにして表示したものを下に示す。
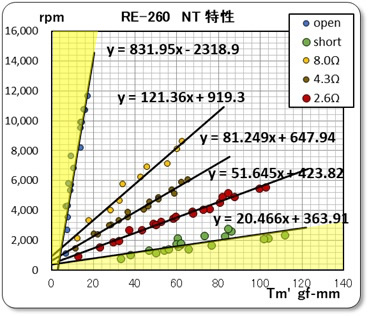
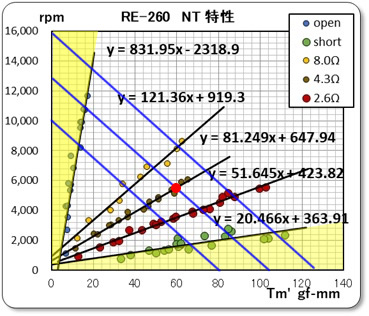
この左のグラフは、上のグラフ2の縦軸と横軸を反転させたものである。
このグラフより、オープン状態( 即ちRb = ∞ )の時と、ショート状態(即ち Rb = 0 )のゾーンが判明できます。そして、黄色のゾーンは、「DCモータのブレーキ制御方法を検討する」(2025/11/22)で説明した調整不可能なゾーンを示しているのだ。 これが当初から求めたかった特性であり、今回のプロジェクトを開始するきっかけとなったグラフである。
**********************************************************
右のグラフは、駆動源としてDCマグネットモータを仮定した時の電圧による制御特性を青色の線で示しました。この駆動モータとブレーキ用のモータを組み合わせた場合は、お互いの特性線が交差する点(赤丸点)にて力がバランスするので、この時のトルクと回転数で安定状態となります。
これは、発電ブレーキとして制御出来ている状態といえます。グラフからもわかるように、2つのモータを適切に選択すれば、お互いの特性がほぼ直角に交差しますので、非常に安定した制御が可能となります。でも、黄色のゾーンでは交差できないので、制御することが不可能なのです。
ここで課題となるのが、ブレーキとして使用するモータの選択と、外部調整する可変抵抗の仕様をどう設定するのかという点です。狙いとする制御範囲に収めるためには、そのための制約条件をしっかりと把握しておくことが必須となります。
■ データの解析 (電圧と回転数の関係より)
今回の実験を始めたきっかけは、上記のブレーキ機能の様子を探る事でしたが、それ以外の解析に目が行ってしまいました。モータを外部から強制的に回転させることによって生じる現象は、モータとしての特性を調べるためにも有効な手段である事を認識した次第です。そこで、色々な観点から解析しでみることにしました。
● 逆起電力 Ke
上記に示すグラフ1より、逆起電力定数 Ke が求められたことは「DCモータのブレーキ特性 RE-260RAのブレーキ特性」(2025/12/2)で示した。
Ke = 0.0002133 volt/rpm
の結果を得ています。
● モータの巻線抵抗 Ra
上記のグラフ1より、外部抵抗Rb の値とグラフの勾配より、モータの巻線抵抗 Ra が求められる。
| Rb | グラフの勾配 | Ra | Raの平均 |
|---|---|---|---|
| 8.0 Ω | 0.00016333 | 2.45 Ω | 1.79 Ω |
| 4.3 Ω | 0.00015978 | 1.44 Ω | |
| 2.6 Ω | 0.00013632 | 1.47 Ω |
でも、バラツキが大きいですね。
■ データの解析 (トルクと回転数の関係より)
この辺から解析作業の迷走が始まりました。
● 軸摩擦トルク Rm と摩擦損失速度係数λm
グラフ2が示しているデータを使って解析作業を実施しました。まず、オープン時のトルクと回転数に注目してそのデータを睨んでいました。この状態は電気が流れていませんので機械的な摩擦、空気抵抗、あるいは磁気的抵抗だけが関係しているはずです。そこで、下に示すように2種類のグラフに加工してみました。
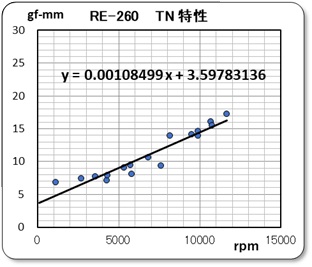
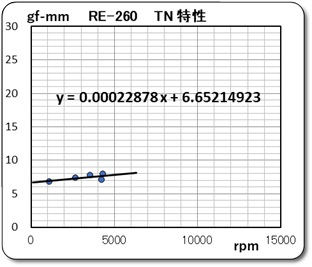
私の定義では、軸摩擦トルク Rm は回転数がゼロの場合、即ちグラフのY切片の値です。また、摩擦損失速度係数λm は直線近似させた場合の勾配として定義していました。そこで、左のグラフは強引に直線近似させた場合です。注億しているゼロ近辺がかけ離れているいるので、小さな値だけに絞って近似させたのが、右のグラフです。こちらの近似式の方が良いと考えて摩擦損失の式を、y = 0.00022878 x + 6.65214923 と近似させ、
- Rm = 6.7 gf-mm と推定
- λm = 0.000229 gf-mm/rpm と推定
しました。
● トルク定数 Kt
次に、上記の値を使用してグラフ2の他のデータのY切片と勾配の値を使って、トルク定数 Kt の値を推定しました。対応した式は先回報告の(7)式です。
| Rb | グラフの勾配 | Y切片 | 勾配−λm | Ra + Rb | Kt・Ke |
Kt | Ktの平均 |
|---|---|---|---|---|---|---|---|
| 2.6 Ω | 0.019054 | -7.11063 | 0.018825 | 4.387 | 0.08259 | 387 | 361 |
| 4.3 Ω | 0.012158 | -737748 | 0.011929 | 6.087 | 0.07261 | 340 | |
| 8.0 Ω | 0.007985 | -6.12923 | 0.007756 | 9.787 | 0.07591 | 356 |
比較のために、上記の Ke の値から 「カタログ値からDCモータの特性値を推定する」(2025/11/23)の(4)式から換算した場合を計算すると、
Kt = 208 gf-mm/A
となります。さらに、同じ報告書にて示したカタログデータからの推定値 Kt = 217.4 gf-mm/A ともズレています。まあ、オーダー的には合っていますけどね。
 .
.
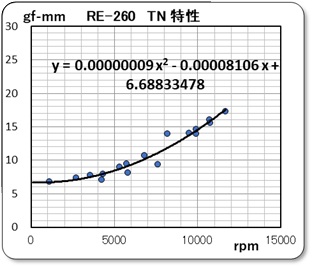
■ 軸の損失項について
軸の摩擦トルクを検討している時、信頼性は薄いとは言いながらも、データは真実を語っていると考えて、2次曲線で近似させたのが右のグラフです。空気抵抗は2次曲線的に上昇するとの知見をどこかで見たからです。なかなかいい感じで近似しています。
そこで、
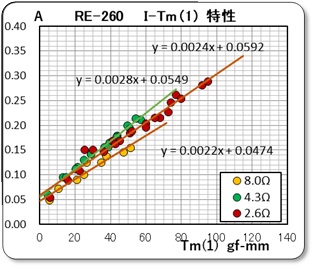
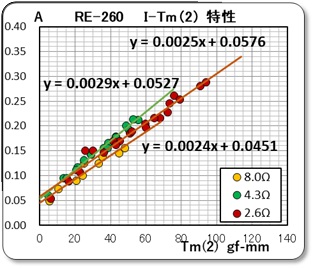
- 測定された軸トルク Tm' に対して
- 損失項を直線近似させて、Tm' から減じたトルクを Tm (1)
- 損失項を2次曲線で近似させて、Tm' から減じたトルクを Tm (2)
として、トルクと電流の特性をプロットしました。
この電流値は、測定されている電圧と抵抗値より電流値を計算したものです。そしてこれをグラフ化したものを下に示すます。、何を期待してこのような解析をしたかと言うと、軸トルクから機械的摩擦項を差し引くと、先回の報告書の(5)式から 回転子に生ずる電気的なトルク Tm の値が求まり、(1)式から Kt の値がダイレクトに求められると考えたからです。
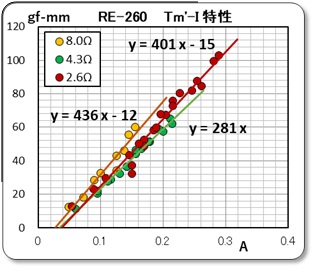
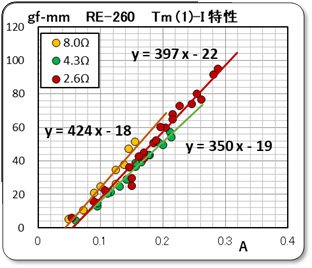
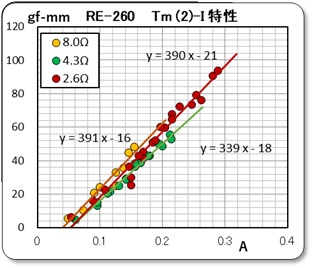
でも、見事に期待が外れました。勾配値は、Kt の値がダイレクトに示しているはずなので、それなりの値を示していますが、原点を通らないのです。電流値が何故だか50mA 近くも損失しているのです。モータの専門家でないのでお手上げです。
そこで、ネットを頼りに調べてみました。すると、モータの測定方法を紹介しているビデオの中で、
- コギングトルクの測定は通電無しでトルクを測定する。
- トルクリップルの測定は通電状態でトルクを測定する。
との情報を見つけました。
通電の有り無しで特性が変わる!
これは新たな認識です。そいえば、グラフ2に於いて、通電無しのオープン状態と、通電ありの他の場合とでは、特にゼロ近辺の様子が異なっています。何かこの辺に自分には未知の領域がありそうです。
********************************************
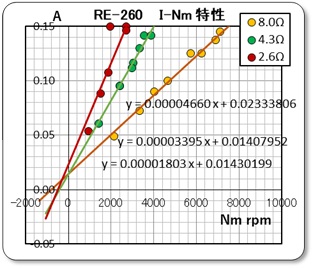
また、トルクリップリの最大値は無負荷時の起動トルクと同等との事でした。このトルクはモータ内部で消費されてしまうので外には出てきませんが、その時に必要な電流は、起動電流として現れてくると考えて、上記のグラフの縦軸と横軸を交換し、トルクゼロ時の電流をY切片として読み取ることにしました。
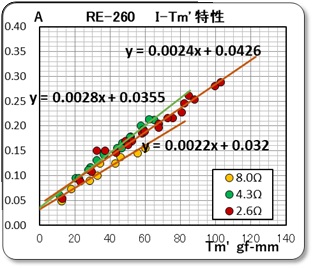
やはり、およそ 50mA の電流値を示していました。そして例のカタログ値では 0.16A 、即ち 160mA と示されていました。
合致しませんね!
折角、このグラフから新な知見を得ることが出来たのでしたが、結果は思わしくありません・・・・・・・・・・・・・。
■ まとめ
当初の狙いであった発電ブレーキとして制御できる範囲とその制御方法について、理解することが出来ましたが、モータとしての特性解析は五里霧中の中に入ってしまいました。そして、自分の未知の領域ではあるが、いろいろ考えてみました。
- 測定方法のどこかに不備があるかも知れない。データが無いのは測定出来ていないのである。
- 知らない重要な要素が解析項に含まれていない。
- ゼロ近辺は非線形領域であるので、線形での解析では無理である。
等々の原因を考えられますが、自分としては次のような認識でいます。
外部から軸にトルクを加えた今回の測定状態では、回転数がゼロの場合、即ちコイルが動いていない状態では、回転子にはフレミングの右手の法則による起電力は発生しません。電圧はゼロで、このため電流もゼロです。そして、軸の静止摩擦(磁石による抵抗力も含む)だけが反応していると考えるからです。すなわち、この機械的な抵抗力を差し引いた状態ではゼロ点を通るはずなのです。でも、グラフからは読み取れないのは、その近辺が測定出来ていないだけなのだと!。
そこで、横軸を回転数に取って、電圧、電流、および出力トルクの値をゼロ点付近を拡大して表示してみました。
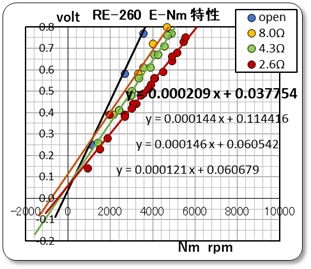
電流と電圧はゼロ近辺までは線形特性に乗ってくるデータなのに、ゼロ点を通らない・・・・・・・。これはまさにゼロ点付近は非線形特性となっていると解釈すべきである。また、トルクの値は電流が流れていないオープン状態に収束しても良いはずなのだが、これも駄目ですね。
**********************************************
ということで、モータの主要な特性は、線形解析で充分に現象を把握することが出来る。しかし、細かい部分を追求しようとするなら、高度な電磁力学の知識と充分な設計ノウハウが必要となり、門外漢には無理な領域である事を理解しました。
**********************************************
このような結果を得たので、今回のプロジェクトは完了という事にしました。何か新しいネタを探すことにしましょう。
2025/12/5