
HOME >> 鉄道模型実験室 > 小型DCモータの調査 ConnモータRF146W
鉄道模型実験室 No.273 小型DCモータの調査 ConnモータRF146W
手持ちの小型DCモータについて、運転準備が整ったのでテスト測定を実施したがまだまだ問題がありました。でも、改善工作の前にシャント抵抗の影響が少なくなる巻線抵抗の大きなモータを使って、もう一度測定を実施してみることにしました。
■ ConnモータRF146W
改善工作の前に巻線抵抗の大きなモータを使って測定を実施してみることにした。選定したモータは、Conn Motor 製のマイクロモータ 6V RF146W-11180-25 モータです。昨年入手したもので、秋月のホームページに仕様等が公開されています。その内容は、
| 定格電圧 | 無負荷 | 定格負荷 | 停止 | 形状 | |||||||
| 回転数 | 電流 | 回転集 | 電流 | 負荷トルク | 負荷出力 | トルク | 電流 | 軸径 | 長さ | 径 | |
| 6 V | 4870 rpm | 0.055 A | 4130 rpm | 0.31 A | 30.5 gf-cm | 1.29 W | 200 gf-cm | 1.7 A | φ2.0 mm | 18 mm | φ22 mm |
です。このカタログデータをもとに特性を計算した結果を「カタログ値からDCモータの特性値を推定する」(2025/11/23)に報告しました。その値を再掲載します。
| 巻線抵抗 | 逆起電力定数 | トルク定数 | 軸摩擦 | 速度係数 |
| Ra | Ke | Kt | Rm | λm |
| 3.53 Ω | 0.001192 volt/rpm | 1161.2 gf-mm/A | -26 gf-mm | 0.018453 gf-mm/rpm |
軸摩擦などの値がマイナスと計算されていますので、少し怪しいですね。でも、巻線抵抗、逆起電力定数、トルク定数などの重要特性値は信頼出来ると考えています。
■ モータの取付
このモータを測定装置のモータ取り付け台に固定します。今までの物よりサイズが大きので、モータ押さえ厚さ 1mm のアルミ板で簡単に作りました。モータ軸にも回転測定用の白黒マーク円盤付きのジョイントを取り付けあした。
白黒マーク円盤の近くに、何時ものフォトリフレクタ(反射タイプ)のTPR-105F 回転数センサを取り付けました。脱着が容易な紙テープを使って固定しています。下左の写真です。そして、この台を測定にセットしました。
測定台への取付が出来ると、関係する配線を実施して、安定化電源とパソコンを用意して測定準備を行います。
測定操作は、安定化電源の電源設定と、測定台操作盤のスイッチ類で実施し、測定はパソコンに表示されるグラフを見ながら進めます。
■ 測定結果
測定された結果を見ていきましょう。今回の測定は「DCモータのブレーキ特性 特性の解析 その1」(2025/12/3)で報告したように、逆起電力定数Ke を簡単に直接測定する方法も実施しました。
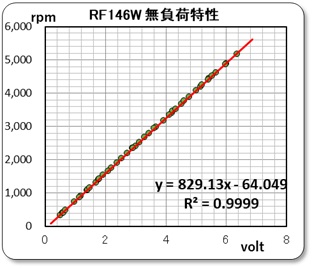
● ジョイント無しの無負荷運転
作動を確認して問題なければ、一度ジョイントを外してモータを無負荷で運転します。
これは、モータの無負荷特性を測定するためと、トルク計のゼロ点チェックを実施するためです。
************************
モータが回転を始める電圧は、正確に測定していませんでしたが、回転を止める直前の値は、0.50ボルトで337rpm の状態まで測定出来ています。なかなか粘りのあるモータのようです。
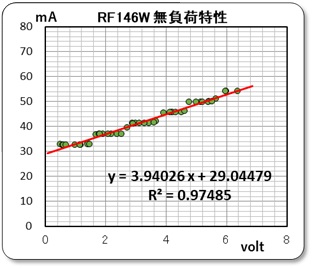
この時の電流も測定していますが、不思議のことに綺麗な階段状になっています。このようなデータは初めてですが何故なのか想像もつきません。手で回すとゴリゴリとかなりのコギングトルクが感じられたので、構造的な特徴があるようです。
● 電気回路をオープンにしての測定
次に、外したジョイントを元に戻し、今度は駆動側モータと負荷側モータの配線を取り換えます。即ち、測定対象のRF146Wモータを負荷側モータにして、強制的に回転させます。この時の電気回路はオープン状態にしておきます。
これは、電気回路がオープンですので電流は流れませんが、モータは強制的に回転させられるので逆起電力が発生するのです。この時の電圧を測定して、逆起電力定数Ke を簡単に測定する手法なのです。
************************************************
電流がゼロの時、発生する電圧Eは、逆起電力定数をKe、ブラシ部電圧降下を Eb 、回転数をとすると、
E = Ke・Nm + Eb
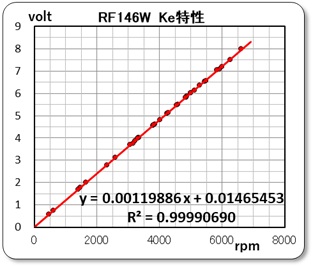
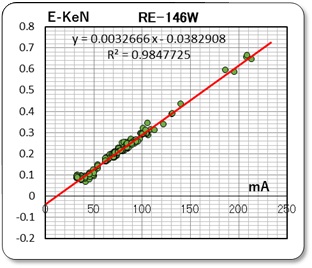
となります。そこで、電圧と回転数のグラフとして右の様の描き、データの近似直線を求めます。
y = 0.001198x + 0.0147
の式の勾配がKe となり、Y切片が電圧降下Eb を示すことになります。即ち、
逆起電力定数 Ke = 0.001199 volt/rpm ブラシ部電圧降下 Eb = 0.01 volt
と読み取ることが出来ます。 Ke の値はカタログ値から求めた値とピッタリですね。 ------- すごいぞ!
そして、 「カタログ値からDCモータの特性値を推定する」(2025/11/23)に示した単位の換算より Kt も計算できます。
トルク定数 Kt = 1167.7 gf-mm/A
となります。
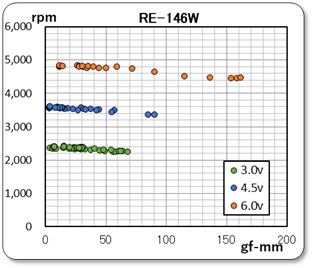
● トルク特性の測定
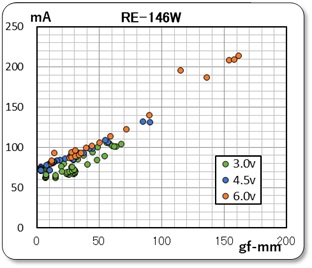
次に、今までと同じ方法にて、供給電圧をパラメータとして、回転数とトルク、および電流とトルクの関係を測定しました。
結果のグラフを右に示します。心配したパラメータ電圧の変動も少なく、今までと同様のグラフを得ることが出来ました。
ただ、ブレーキ式の今までの負荷装置のように負荷状態を微調整するのが困難でした。また、負荷回路をオープン状態とクローズド状態にしても、グラフに示すような範囲しか測定できませんでした。
負荷側のモータは、もっとパワーのある(しっかりとブレーキを掛けることが出来る)モータにする必要がありそうです。
● モータ特性の解析
測定で得られたこれらのデータをもとにして、特性値を求めるべき解析を実施しました。その方法は、「モータ特性のモデル化 改良版」(2016/10/26)あるいは、「モータ特性の測定とモデル化 モータ定数の推定方法」(2019/5/23)にて説明しましたが、今回は少し変更して実施しました。
その中の、電圧に関する関係式から定数 Ke 、Ra 、Eb の最適値をそれぞれ推定するとして、
δ = E - Ra・I = Ke・Nm + Eb
の式を使用し、3個の未知数の最適解を逐次金法まがいの手法で求めていました。今回は、その中の Ke の値がすでに求められていますので、
E - Ke・Nm = Ra・I + Eb
とすれば、左辺のデータが計算できます。そこでこの計算したデータをグラフ化し、その勾配とY切片を読み取れば、巻線抵抗Raとブラシ部電圧降下Eb を、ダイレクトに読み取ることが出来るのです。
その結果を右のグラフにしめします。このグラフより、mA をA の単位に換算しなおして
巻線抵抗Ra = 3.27 Ω 電圧降下Eb = 0.03volt
と読み取れます。これらの値は、カタログから計算した値とか上記で求めた値とほぼ同じですね。
*******************************************************
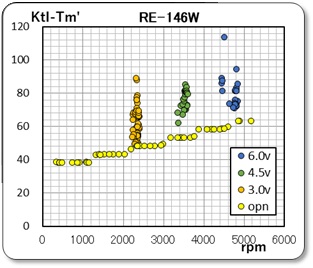
そして、次の トルクに関する関係式から定数 Kt 、Rm 、λm の最適値をそれぞれ推定するにならって、Kt・I - Tm' の値を計算しグラフ化しました。すると今まで見たことない様子を呈することになったのです。
この値、即ちトルク損失は回転数と関係するとした考えでグラフ化したのが左のグラフですが、その関係を見出せませんでした。
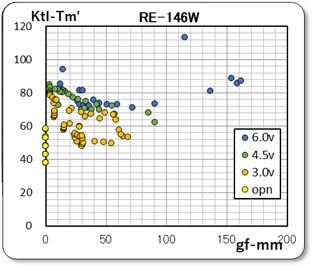
そこで、今度はトルク値との関係を見るため、右のグラフのような表示にしてみました。グラフより、下に凹んだ関係の様ですし、ある一定ではあるものの、低トルクではバラツキが大きいのだと言う意味にも取れます。
これらは、摩擦トルクの原因がよくわかっていないため、断定することができません。そこで思い切って摩擦抵抗値は速度項とトルク項があり、それぞれ速度、あるいはトルクに依存するトルク損失であると仮定することにしました。
即ち、 摩擦抵抗値 = 速度項 + トルク項 と仮定しました。
速度項は、トルクがゼロの状態、即ち無負荷時の状態の動向と考え、この時の電圧と電流の関係より、電流値 = 軸摩擦損失トルクとして算定することにした。即ち、無負荷特性の電流グラフより y = 3.94026x + 29.04479 の換算式を使って、その時の無負荷相当の電流を求め、トルク定数Kt よりトルク値に換算しました。
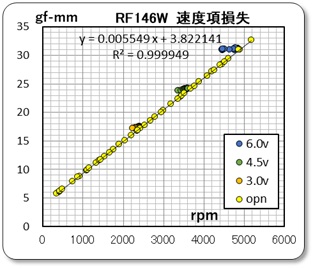
こうして求めたトルクデータを速度項損失として、回転数を横軸にしてグラフ化したものを下左に示す。この時の勾配とY切片が速度係数λmであり、Y切片が摩擦トルクとすると、
摩擦トルク Rm = 3.8gf-mm 摩擦損失速度係数 λm = 0.00555
となります。
さらに、上記で計算した Kt・I - Tm' の値よりこの速度項を差し引いたのがトルク項と考えて、その計算した結果を下中のグラフです。
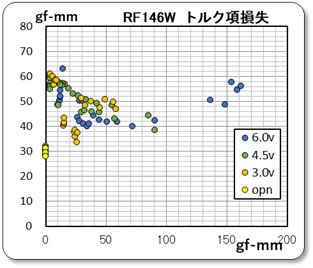
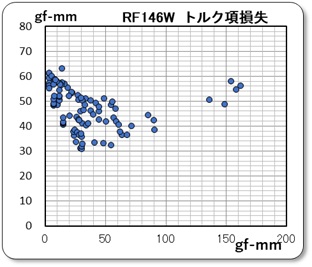
でも、このグラフからは全体のバラツキは少し収まったものの、摩擦トルクの傾向を読み取れません。そこで、速度項とした無負荷時のデータを除いた全てのデータを右のグラフに示しますが、出力トルクとの関係が見出せなかったので、全体の平均値を求めて、一定値とすることにしました。この一定値、47.53 gf-mm の値を速度項の一定値と合算して摩擦トルクとしました。即ち、
摩擦トルク Rm = 51.35 gf-mm 摩擦損失速度係数 λm = 0.005549
と断定しました。 カタログ値から計算した値とは大きくかけ離れてしまいました・・・・・・・・。
■ 推定特性値よりカタログに示された特性と比較する
このように推定してきた特性値は、カタログに示された値と合致するのか検証することにしました。
その方法は、「モータ特性のモデル化 改良版」(2016/10/25)の式を使用し、無負荷時の回転数と電流、およびストール時のトルクと電流を計算しました。
| 電圧 6V | 無負荷時 | ストール時 | ||
|---|---|---|---|---|
| 回転数 | 電流 | トルク | 電流 | |
| カタログデータ | 4870 rpm | 0.055 A | 200 gf-cm | 1.7 A |
| 推定計算値 | 4829 rpm | 0.060 A | 2070 gf-mm | 1.832 A |
なかなかいい線を言っていますね。シメシメです。
************************************************
また、定格とは、いろいろな定義があるので一概に決めることが出来ません。最大出力の時なのか、最大効率の時なのか、あるいはモータの発熱限界を考えた30分定格とか1時間定格などもあります。あるいは長時間の連続使用も許容される条件などもありますので、今回はこれらのデータ不足により判断出来ません。
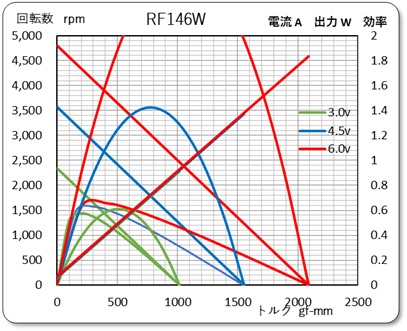
また、「モータ特性の測定とモデル化 データのまとめと比較」(2019/5/27)に示した方法にて、効率や出力なども計算してみました。その結果を右のグラフに示します。
このグラフを見ている時、カタログで言う定格とは、最大効率の状態を言っているものと推定しました。ちなみに、推定した特性値から最大効率の値を計算してみると、 回転数 404 1rpm 電流 0.35 A 負荷トルク 334 gf-mm 負荷出力 1.39 w と計算されましたが、カタログの定格値と合ってきましたね。
■ まとめ
思っていたよりも、カタログ値に近いデータを取得することが出来ました。おっかなびっくりで始めた自分の測定に少し自信がついてきました。
- 以前、苦労して解析した手法よりもズーと簡単に実施出来ました。これは、特性値推定の基本となっている逆起電力定数Ke を測定する手法が、簡単ではあるが、正確でかつ信頼のある方法であることによる効果と考えています。
- 今回の方法では、パラメータとして設定した電圧の値を固定する意味が無いことが分かります。グラフとしての見栄えはあるのですが、特性値の推定値には必要なかった条件だったのです。このことは、シャント抵抗が云々という配慮が必要ないことを意味します。
- メーカーが公表しているカタログデータは、ある代表製品の測定結果なのか、あるいは設計値なのかは分かりませんが、製品自身のバラツキを考えても信頼できるデータである事を認識しました。
- 今回の手法を標準として、気楽に他のモータについても測定してみたくなりました。目的不明のホビーの楽しみですね。
********************************************
次回は、他のモータの測定結果を報告しましょう。
2026/1/14